Analysing head-direction cells#
This tutorial demonstrates how we use Pynapple to generate Figure 4a in the publication. The NWB file for the example is hosted on OSF. We show below how to stream it. The entire dataset can be downloaded here.
import scipy
import pandas as pd
import numpy as np
import pynapple as nap
import matplotlib.pyplot as plt
import seaborn as sns
import requests, os
import xarray as xr
custom_params = {"axes.spines.right": False, "axes.spines.top": False}
sns.set_theme(style="ticks", palette="colorblind", font_scale=1.5, rc=custom_params)
xr.set_options(display_expand_attrs=False)
Downloading the data#
It’s a small NWB file.
path = "Mouse32-140822.nwb"
if path not in os.listdir("."):
r = requests.get(f"https://osf.io/jb2gd/download", stream=True)
block_size = 1024*1024
with open(path, 'wb') as f:
for data in r.iter_content(block_size):
f.write(data)
Parsing the data#
The first step is to load the data and other relevant variables of interest.
data = nap.load_file(path) # Load the NWB file for this dataset
What does this look like?
print(data)
Mouse32-140822
┍━━━━━━━━━━━━━━━━━━━━━━━┯━━━━━━━━━━━━━┑
│ Keys │ Type │
┝━━━━━━━━━━━━━━━━━━━━━━━┿━━━━━━━━━━━━━┥
│ units │ TsGroup │
│ sws │ IntervalSet │
│ rem │ IntervalSet │
│ position_time_support │ IntervalSet │
│ epochs │ IntervalSet │
│ ry │ Tsd │
┕━━━━━━━━━━━━━━━━━━━━━━━┷━━━━━━━━━━━━━┙
Head-Direction Tuning Curves#
To plot head-direction tuning curves, we need the spike timings and the orientation of the animal. These quantities are stored in the variables ‘units’ and ‘ry’.
spikes = data["units"] # Get spike timings
epochs = data["epochs"] # Get the behavioural epochs (in this case, sleep and wakefulness)
angle = data["ry"] # Get the tracked orientation of the animal
What does this look like?
print(spikes)
Index rate location group
------- ------- ---------- -------
0 2.96981 thalamus 1
1 2.42638 thalamus 1
2 5.93417 thalamus 1
3 5.04432 thalamus 1
4 0.30207 adn 2
5 0.87042 adn 2
6 0.36154 adn 2
... ... ... ...
42 1.02061 thalamus 5
43 6.84913 thalamus 6
44 0.94002 thalamus 6
45 0.55768 thalamus 6
46 1.15056 thalamus 6
47 0.46084 thalamus 6
48 0.19287 thalamus 7
Here, rate is the mean firing rate of the unit. Location indicates the brain region the unit was recorded from, and group refers to the shank number on which the cell was located.
This dataset contains units recorded from the anterior thalamus. Head-direction (HD) cells are found in the anterodorsal nucleus of the thalamus (henceforth referred to as ADn). Units were also recorded from nearby thalamic nuclei in this animal. For the purposes of our tutorial, we are interested in the units recorded in ADn. We can restrict ourselves to analysis of these units rather easily, using Pynapple.
spikes_adn = spikes.getby_category("location")["adn"] # Select only those units that are in ADn
print(spikes_adn)
Index rate location group
------- -------- ---------- -------
4 0.30207 adn 2
5 0.87042 adn 2
6 0.36154 adn 2
7 10.51737 adn 2
8 2.62475 adn 2
9 2.55818 adn 2
10 7.06715 adn 2
... ... ... ...
28 1.78011 adn 4
29 4.23006 adn 4
30 2.15215 adn 4
31 0.58829 adn 4
32 1.12899 adn 4
33 5.26316 adn 4
34 1.57122 adn 4
Let’s compute some head-direction tuning curves. To do this in Pynapple, all you need is a single line of code!
tuning_curves = nap.compute_tuning_curves(
data=spikes_adn,
features=angle,
bins=61,
epochs=epochs[epochs.tags == "wake"],
range=(0, 2 * np.pi),
feature_names=["head_direction"]
)
tuning_curves
<xarray.DataArray (unit: 31, head_direction: 61)> Size: 15kB
array([[ 0.25516826, 0.30063079, 0.18988237, ..., 0. ,
0. , 0.0676977 ],
[ 0.12758413, 0. , 0.09494118, ..., 0.11227404,
0.13800704, 0.10154655],
[ 0.17011218, 0.18789424, 0.09494118, ..., 0.02806851,
0.16560845, 0.13539541],
...,
[ 0.46780848, 0.37578848, 0.15823531, ..., 0.36489062,
0.3312169 , 0.54158162],
[ 5.27347746, 8.38008318, 10.50682437, ..., 0.95432931,
1.02125211, 2.23402419],
[ 1.78617785, 1.95410011, 3.89258855, ..., 0.19647956,
0.44162253, 0.60927932]], shape=(31, 61))
Coordinates:
* unit (unit) int64 248B 4 5 6 7 8 9 10 11 ... 28 29 30 31 32 33 34
* head_direction (head_direction) float64 488B 0.0515 0.1545 ... 6.129 6.232
Attributes: (3)The output is an xarray.DataArray with one dimension representing units, and another for head-direction angles.
Computing information and selecting HD cells#
We can use compute_mutual_information to compute the mutual information between the activity of each unit and the head direction of the mouse:
MI = nap.compute_mutual_information(tuning_curves)
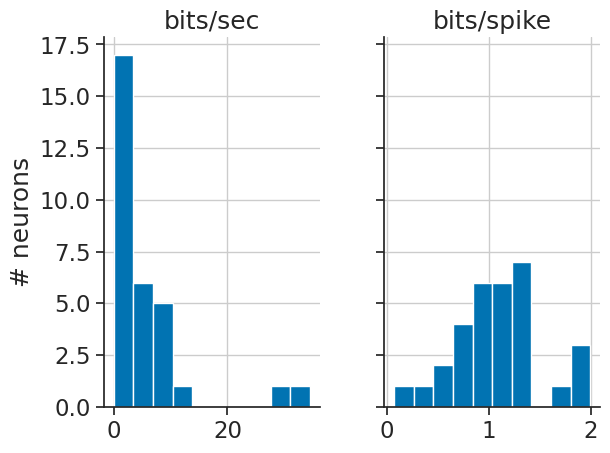
We can use this as a score to select the neurons that are most modulated by HD:
top_n = 20
best_neurons = MI.sort_values(by="bits/sec", ascending=False).head(top_n).index
tuning_curves = tuning_curves.sel(unit=best_neurons).sortby("unit")
spikes_adn = spikes_adn[best_neurons]
best_neurons
Index([24, 18, 22, 7, 14, 20, 29, 33, 21, 25, 26, 17, 10, 13, 34, 23, 30, 12,
9, 31],
dtype='int64')
We can then compute the preferred angle of every neuron quickly as follows:
pref_ang = tuning_curves.idxmax(dim="head_direction")
For easier visualization, we will color our plots according to the preferred angle of the cell. To do so, we will normalize the range of angles we have, over a colormap.
# Normalizes data into the range [0,1]
norm = plt.Normalize()
# Assigns a color in the HSV colormap for each value of preferred angle
color = plt.cm.hsv(norm([i / (2 * np.pi) for i in pref_ang.values]))
color = xr.DataArray(
color,
dims=("unit", "color"),
coords={"unit": pref_ang.unit}
)
To make the tuning curves look nice, we will smooth them before plotting:
tuning_curves.values = scipy.ndimage.gaussian_filter1d(
tuning_curves.values,
sigma=3,
axis=1,
mode="wrap" # important for circular variables!
)
What does this look like? Let’s plot them!
sorted_tuning_curves = tuning_curves.sortby(pref_ang)
plt.figure(figsize=(12, 9))
for i, n in enumerate(sorted_tuning_curves.coords["unit"]):
# Plot the curves in 8 rows and 4 columns
plt.subplot(8, 4, i + 1, projection='polar')
plt.plot(
sorted_tuning_curves.coords["head_direction"],
sorted_tuning_curves.sel(unit=n).values,
color=color.sel(unit=n).values
) # Colour of the curves determined by preferred angle
plt.xticks([])
plt.show()
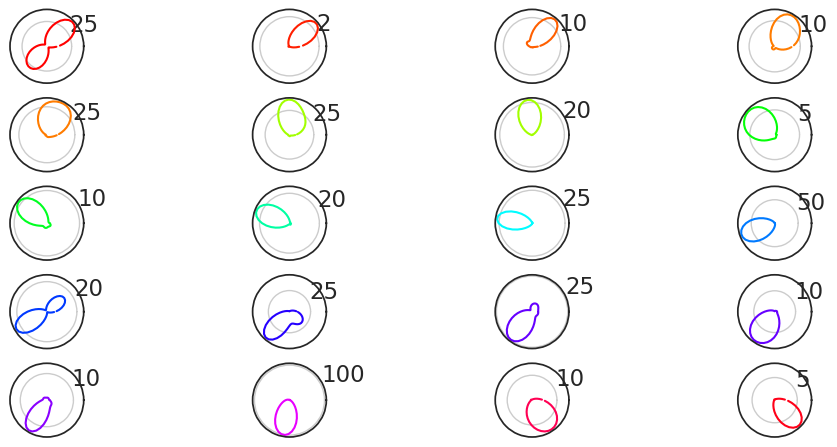
Awesome!
Decoding#
Now that we have HD tuning curves, we can go one step further. Using only the population activity of ADn units, we can decode the direction the animal is looking in. We will then compare this to the real head-direction of the animal, and discover that population activity in the ADn indeed codes for HD.
To decode the population activity, we will be using a bayesian decoder as implemented in Pynapple. Again, just a single line of code:
decoded, proba_feature = nap.decode_bayes(
tuning_curves=tuning_curves,
data=spikes_adn,
epochs=epochs[epochs.tags == "wake"],
bin_size=0.1,
)
What does this look like?
print(decoded)
Time (s)
---------- ---------
8812.35 0.772523
8812.45 0.66952
8812.55 0.463514
8812.65 0.66952
8812.75 0.566517
8812.85 0.66952
8812.95 0.566517
...
10770.65 0.0515015
10770.75 5.92267
10770.85 5.71667
10770.95 5.81967
10771.05 5.81967
10771.15 5.92267
10771.25 5.81967
dtype: float64, shape: (19590,)
The variable decoded contains the most probable angle, and proba_feature contains the probability of a given angular bin at a given time point:
print(proba_feature)
Time (s) 0.05150151891130808 0.15450455673392424 0.2575075945565404 0.3605106323791566 0.4635136702017727 ...
---------- --------------------- --------------------- -------------------- -------------------- -------------------- -----
8812.35 3.48835e-05 0.00059806 0.00533339 0.0260361 0.0746997 ...
8812.45 2.21735e-05 0.000614683 0.00743133 0.0418445 0.122353 ...
8812.55 0.00999712 0.0486365 0.129685 0.204767 0.213704 ...
8812.65 0.00020852 0.00270902 0.0179733 0.0648892 0.140203 ...
8812.75 0.000952719 0.00872301 0.0421837 0.114205 0.189812 ...
8812.85 0.000248298 0.00325789 0.0208956 0.0710574 0.143999 ...
8812.95 0.000594774 0.00691987 0.0391238 0.115574 0.198835 ...
... ...
10770.65 0.199764 0.166134 0.104828 0.0546868 0.0262783 ...
10770.75 0.0234972 0.00694568 0.00164996 0.000346505 7.24936e-05 ...
10770.85 0.000837917 7.95057e-05 5.39872e-06 2.97754e-07 1.58265e-08 ...
10770.95 0.00125775 0.000123647 8.61334e-06 4.88387e-07 2.7256e-08 ...
10771.05 0.00304119 0.000493517 6.31983e-05 7.19529e-06 8.44358e-07 ...
10771.15 0.0148238 0.00331142 0.000558963 7.90331e-05 1.07205e-05 ...
10771.25 0.00353907 0.000478658 4.6702e-05 3.7137e-06 2.82474e-07 ...
dtype: float64, shape: (19590, 61)
Each row is a time bin, and each column is an angular bin. The sum of all values in a row add up to 1.
Now, let’s plot the raster plot for a given period of time, and overlay the actual and decoded HD on the population activity.
ep = nap.IntervalSet(
start=10717, end=10730
) # Select an arbitrary interval for plotting
plt.subplots(figsize=(12, 6))
plt.rc("font", size=12)
for i, n in enumerate(spikes_adn.keys()):
plt.plot(
spikes[n].restrict(ep).fillna(pref_ang.sel(unit=n).item()), "|", color=color.sel(unit=n).values
) # raster plot for each cell
plt.plot(
decoded.restrict(ep), "--", color="grey", linewidth=2, label="decoded HD"
) # decoded HD
plt.legend(loc="upper left")
plt.xlabel("Time (s)")
plt.ylabel("Neurons")
plt.show()
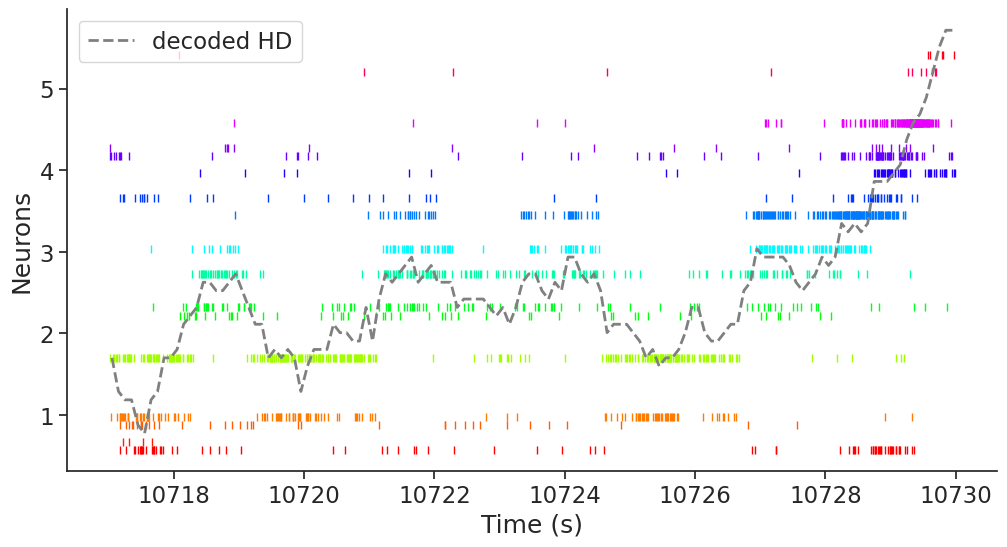
From this plot, we can see that the decoder is able to estimate the head-direction based on the population activity in ADn.
We can also visualize the probability distribution. Ideally, the bins with the highest probability correspond to the bins with the most spikes.
smoothed = scipy.ndimage.gaussian_filter(
proba_feature, 1
) # Smoothing the probability distribution
# Create a DataFrame with the smoothed distribution
p_feature = pd.DataFrame(
index=proba_feature.index.values,
columns=proba_feature.columns.values,
data=smoothed,
)
p_feature = nap.TsdFrame(p_feature) # Make it a Pynapple TsdFrame
plt.figure()
plt.plot(
angle.restrict(ep), "w", linewidth=2, label="actual HD", zorder=1
) # Actual HD, in white
plt.plot(
decoded.restrict(ep), "--", color="grey", linewidth=2, label="decoded HD", zorder=1
) # Decoded HD, in grey
# Plot the smoothed probability distribution
plt.imshow(
np.transpose(p_feature.restrict(ep).values),
aspect="auto",
interpolation="bilinear",
extent=[ep["start"][0], ep["end"][0], 0, 2 * np.pi],
origin="lower",
cmap="viridis",
)
plt.xlabel("Time (s)") # X-axis is time in seconds
plt.ylabel("Angle (rad)") # Y-axis is the angle in radian
plt.colorbar(label="probability")
plt.show()
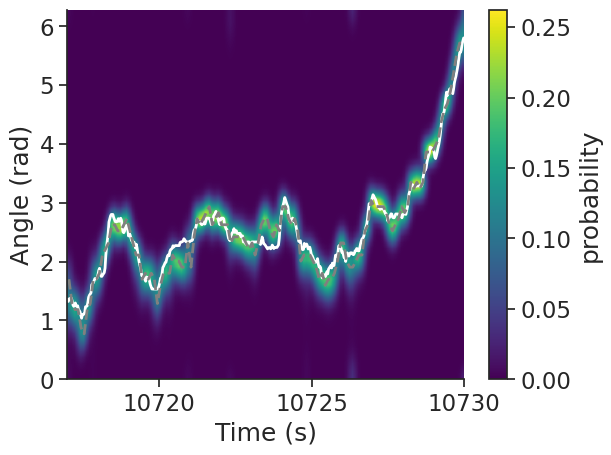
The decoded HD (dashed grey line) closely matches the actual HD (solid white line), and thus the population activity in ADn is a reliable estimate of the heading direction of the animal.
I hope this tutorial was helpful. If you have any questions, comments or suggestions, please feel free to reach out to the Pynapple Team!
Authors
Wolf de Wulf
Dhruv Mehrotra
Guillaume Viejo