Correlograms & ISI#

Hide code cell content

 
import pynapple as nap
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
custom_params = {"axes.spines.right": False, "axes.spines.top": False}
sns.set_theme(style="ticks", palette="colorblind", font_scale=1.5, rc=custom_params)

Let’s generate some data. Here we have two neurons recorded together. We can group them in a TsGroup.

ts1 = nap.Ts(t=np.sort(np.random.uniform(0, 1000, 2000)), time_units="s")
ts2 = nap.Ts(t=np.sort(np.random.uniform(0, 1000, 1000)), time_units="s")
epoch = nap.IntervalSet(start=0, end=1000, time_units="s")
ts_group = nap.TsGroup({0: ts1, 1: ts2}, time_support=epoch)
print(ts_group)

  Index    rate
-------  ------
      0       2
      1       1

Autocorrelograms#

We can compute their autocorrelograms meaning the number of spikes of a neuron observed in a time windows centered around its own spikes. For this we can use the function compute_autocorrelogram. We need to specifiy the binsize and windowsize to bin the spike train.

autocorrs = nap.compute_autocorrelogram(
    group=ts_group, binsize=100, windowsize=1000, time_units="ms", ep=epoch  # ms
)
print(autocorrs)

           0     1
-0.9  1.0325  0.91
-0.8  1.0425  0.94
-0.7  0.9575  1.08
-0.6  1.0075  1.06
-0.5  0.8975  1.01
-0.4  0.9050  0.98
-0.3  0.9475  1.00
-0.2  1.0750  0.97
-0.1  1.0500  1.07
 0.0  0.0000  0.00
 0.1  1.0500  1.07
 0.2  1.0750  0.97
 0.3  0.9475  1.00
 0.4  0.9050  0.98
 0.5  0.8975  1.01
 0.6  1.0075  1.06
 0.7  0.9575  1.08
 0.8  1.0425  0.94
 0.9  1.0325  0.91

The variable autocorrs is a pandas DataFrame with the center of the bins for the index and each column is an autocorrelogram of one unit in the TsGroup.

Cross-correlograms#

Cross-correlograms are computed between pairs of neurons.

crosscorrs = nap.compute_crosscorrelogram(
    group=ts_group, binsize=100, windowsize=1000, time_units="ms"  # ms
)
print(crosscorrs)

          0
          1
-0.9  0.965
-0.8  1.070
-0.7  0.980
-0.6  0.925
-0.5  1.005
-0.4  1.005
-0.3  0.940
-0.2  1.000
-0.1  1.030
 0.0  0.960
 0.1  0.925
 0.2  0.975
 0.3  1.050
 0.4  0.960
 0.5  1.040
 0.6  1.070
 0.7  0.985
 0.8  1.045
 0.9  0.890

Column name (0, 1) is read as cross-correlogram of neuron 0 and 1 with neuron 0 being the reference time.

Event-correlograms#

Event-correlograms count the number of event in the TsGroup based on an event timestamps object.

eventcorrs = nap.compute_eventcorrelogram(
    group=ts_group, event = nap.Ts(t=[0, 10, 20]), binsize=0.1, windowsize=1
    )
print(eventcorrs)

             0         1
-0.9  0.000000  2.777778
-0.8  1.257862  0.000000
-0.7  1.257862  5.555556
-0.6  1.257862  0.000000
-0.5  0.000000  0.000000
-0.4  1.257862  0.000000
-0.3  0.000000  0.000000
-0.2  1.257862  0.000000
-0.1  1.257862  0.000000
 0.0  0.000000  2.777778
 0.1  1.257862  0.000000
 0.2  0.000000  2.777778
 0.3  0.000000  2.777778
 0.4  2.515723  0.000000
 0.5  0.000000  0.000000
 0.6  1.257862  0.000000
 0.7  0.000000  0.000000
 0.8  0.000000  2.777778
 0.9  2.515723  0.000000

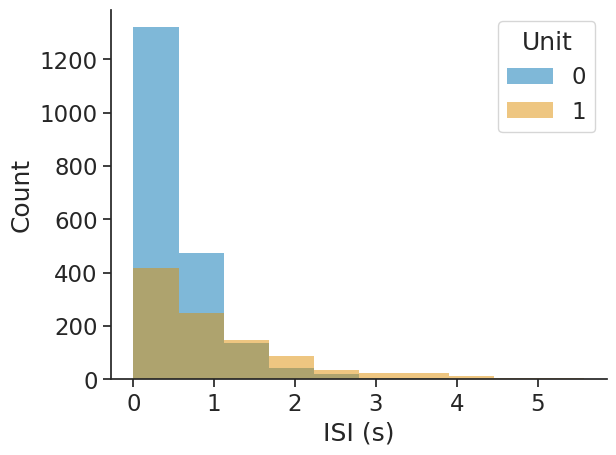
Interspike interval (ISI) distribution#

The interspike interval distribution shows how the time differences between subsequent spikes (events) are distributed. The input can be any object with timestamps. Passing epochs restricts the computation to the given epochs. The output will be a dataframe with the bin centres as index and containing the corresponding ISI counts per unit.

isi_distribution = nap.compute_isi_distribution(
    data=ts_group, bins=10, epochs=epoch
    )
print(isi_distribution)

             0    1
0.279448  1321  418
0.837100   472  247
1.394752   136  146
1.952403    43   86
2.510055    19   36
3.067707     3   25
3.625359     5   23
4.183010     0   11
4.740662     0    4
5.298314     0    3

Hide code cell source

 
for col in isi_distribution.columns:
    plt.bar(
        isi_distribution.index,
        isi_distribution[col].values,
        width=np.diff(isi_distribution.index).mean(),
        alpha=0.5,
        label=col,
        align='center',
        edgecolor='none'
    )
plt.xlabel("ISI (s)")
plt.ylabel("Count")
plt.legend(title="Unit")
plt.show()
../_images/df6418a91d49c88948c2f11b1fe1608aca9bf466e0648c640e9cb40cc3ca9f0c.png

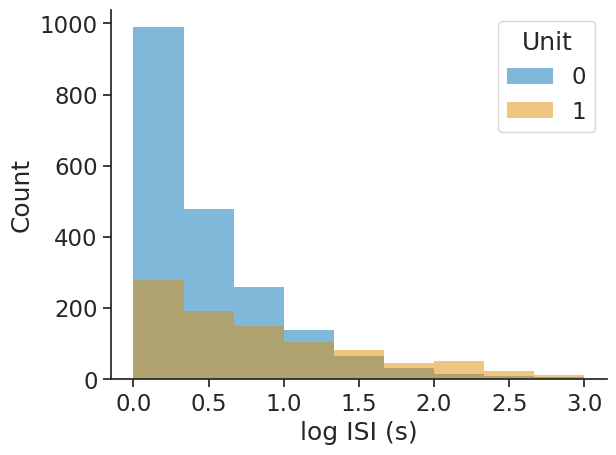
The bins argument allows for choosing either the number of bins as an integer or the bin edges as an array directly:

isi_distribution = nap.compute_isi_distribution(
    data=ts_group, bins=np.linspace(0, 3, 10), epochs=epoch
    )
print(isi_distribution)

            0    1
0.166667  989  280
0.500000  479  193
0.833333  259  149
1.166667  138  106
1.500000   64   83
1.833333   31   46
2.166667   16   50
2.500000   10   22
2.833333    6   11

Hide code cell source

 
for col in isi_distribution.columns:
    plt.bar(
        isi_distribution.index,
        isi_distribution[col].values,
        width=np.diff(isi_distribution.index).mean(),
        alpha=0.5,
        label=col,
        align='center',
        edgecolor='none'
    )
plt.xlabel("log ISI (s)")
plt.ylabel("Count")
plt.legend(title="Unit")
plt.show()
../_images/e83369588556bd1e422f7c157cf45c36992079328eae0e2fbd6e7a1fd46c2e9c.png

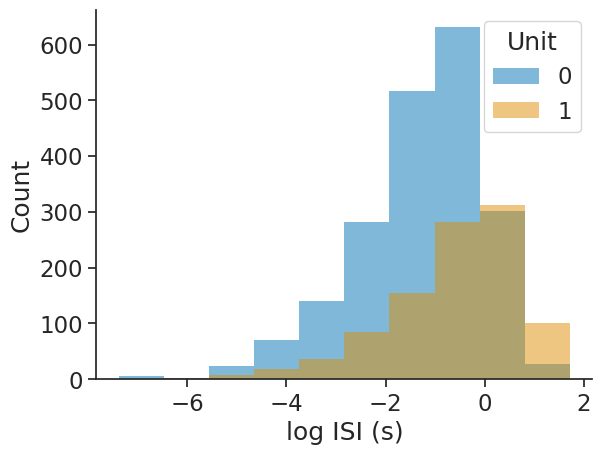
The log_scale argument allows for applying the log-transform to the ISIs:

isi_distribution = nap.compute_isi_distribution(
    data=ts_group, bins=10, log_scale=True, epochs=epoch
    )
print(isi_distribution)

             0    1
-6.927166    6    0
-6.017077    3    2
-5.106989   23    8
-4.196900   70   19
-3.286811  140   36
-2.376723  281   85
-1.466634  516  154
-0.556546  631  282
 0.353543  302  312
 1.263632   27  101

Hide code cell source

 
for col in isi_distribution.columns:
    plt.bar(
        isi_distribution.index,
        isi_distribution[col].values,
        width=np.diff(isi_distribution.index).mean(),
        alpha=0.5,
        label=col,
        align='center',
        edgecolor='none'
    )
plt.xlabel("log ISI (s)")
plt.ylabel("Count")
plt.legend(title="Unit")
plt.show()
../_images/b303fb4c16a9e55f6de1b2619a09a69cded089900dacf219349333be2736d9ed.png